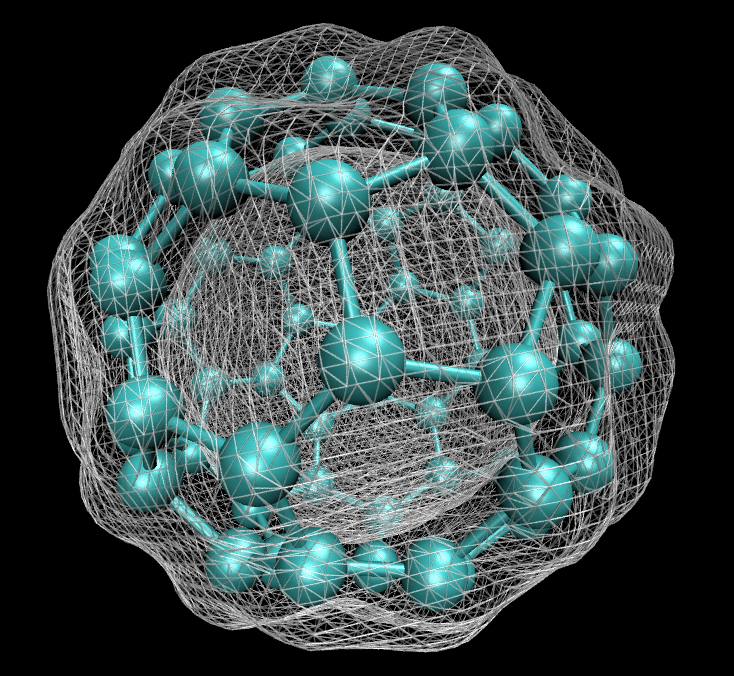
In this work, we propose a deep learning approach to KS-DFT. We propose to directly minimize the total energy by reparameterizing the orthogonal constraint as a feed-forward computation. We prove that such an approach has the same expressivity as the SCF method, yet reduces the computational complexity from O(N^4) to O(N^3).
Tianbo Li
Tianbo Li is currently working as a research scientist at SEA AI Lab, where his primary research area is AI for Quantum Chemistry and Material Science. He obtained his Ph.D from Nanyang Technological University, Singapore, under the supervison of Prof. Yiping Ke. Prior to that, he received both his degrees of Bacholer and Master from the School of Statistcs, Renmin University of China. Collaborating closely with Prof. Konstantin S. Novoselov, Tianbo is actively involved with Institute for Functional Intelligent Materials (I-FIM), National University of Singapore. Besides his focus on AI for Science, he also has a keen interest in statistical machine learning and exploring stochastic processes for deep learning.
We are currently hiring research interns working on AI for Science (Quantum Chemistry), based in Singapore.
To learn more about our research, please see and apply via the following link:
If you find this position interested, feel free to email me your CV for consideration.
Education
-
Nanyang Technological University, Singapore
Ph.D in Computer Science
2017.1 - 2021.2, Singapore -
Renmin University of China
M.Econ in Risk Management and Actuarial Science
2014.9 - 2017.1, Beijing, China -
Renmin University of China
B.S in Statistics
2010.9 - 2014.6, Beijing, China
Project
ICLR 2023 (Spotlight)
D4FT: A Deep Learning Approach to Kohn-Sham Density Functional Theory
ICML 2023
Nonparametric Generative Modeling with Conditional Sliced-Wasserstein Flows
In this work, we make two major contributions to bridging this gap. Based on a pleasant observation that (under certain conditions) the SWF of joint distributions coincides with those of conditional distributions, we propose CSWF that enables nonparametric conditional modeling. We introduce appropriate inductive biases of images into SWF which greatly improve the efficiency and quality of modeling images.
ICLR 2023 Workshop Physics4ML
Neural Integral Functionals
In this work, we propose neural integral functional (NIF), which is a general functional approximator that suits a large number of scientific problems including the brachistochrone curve problem in classical physics and density functional theory in quantum physics.
SIGKDD 2021
Mitigating Performance Saturation in Neural Marked Point Processes: Architectures and Loss Functions
This work introduces a Graph Convolutional Hawkes Process (GCHP) method incorperating marked point processes model to deal with predictions on attributed event sequences.
AAAI 2020
Tweedie-Hawkes Processes: Interpreting the Phenomena of Outbreaks
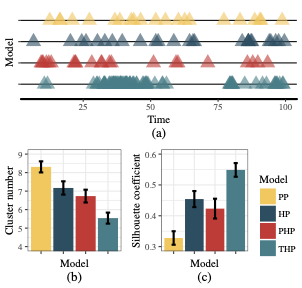
In this paper, we propose a Bayesian model called Tweedie-Hawkes Processes (THP), which is able to model the outbreaks of events and find out the dominant factors behind. THP leverages on the Tweedie distribution in capturing various excitation effects. A variational EM algorithm is developed for model inference.
NeurIPS 2019
Thinning for Accelerating the Learning of Point Processes
This paper discusses one of the most fundamental issues about point processes that what is the best sampling method for point processes. We propose thinning as a downsampling method for accelerating the learning of point processes. We find that the thinning operation preserves the structure of intensity, and is able to estimate parameters with less time and without much loss of accuracy.
ICDM 2018
Transfer hawkes processes with content information
In this paper,we propose a novel model called transfer Hybrid Least Square for Hawkes (trHLSH) that incorporates Hawkes processes with content and cross-domain information.